http://hi.baidu.com/hehui1500/item/fba9444327a24693823ae1e9
(参考文章)
标准差和方差一般是用来描述一维数据的
所谓的维数,拿EEG信号来说,每个通道就是一个维度,而同一个通道的每个一数字是样本。
协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义:
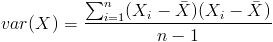
来度量各个维度偏离其均值的程度,标准差可以这么来定义:

从协方差的定义上我们也可以看出一些显而易见的性质,如:
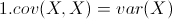
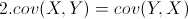
协方差多了就是协方差矩阵
这个定义还是很容易理解的,我们可以举一个简单的三维的例子,假设数据集有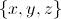 三个维度,则协方差矩阵为
三个维度,则协方差矩阵为
其中cov(x,y)就是一个数,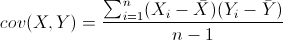 对应x,y渠道平均值后,求内积再求平均值,就是x,y之间的协方差
对应x,y渠道平均值后,求内积再求平均值,就是x,y之间的协方差
可见,协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。
Matlab协方差实战
协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。
这个我将结合下面的例子说明,以下的演示将使用Matlab,为了说明计算原理,不直接调用Matlab的cov函数 。
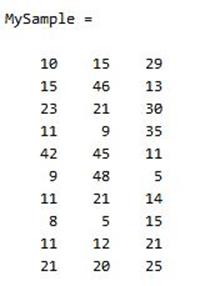
首先,随机产生一个10*3维的整数矩阵作为样本集,10为样本的个数,3为样本的维数。
1MySample = fix(rand(10,3)*50)
根据公式,计算协方差需要计算均值,那是按行计算均值还是按列呢,我一开始就老是困扰这个问题。前面我们也特别强调了,协方差矩阵是计算不同维度间的协方差,要时刻牢记这一点。样本矩阵的每行是一个样本,每列为一个维度,所以我们要按列计算均值。
dim1 = MySample(:,1);dim2 = MySample(:,2);dim3 = MySample(:,3);
计算dim1与dim2,dim1与dim3,dim2与dim3的协方差:
sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 ) % 得到 74.5333
sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -10.0889
sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -106.4000
搞清楚了这个后面就容易多了,协方差矩阵的对角线就是各个维度上的方差,下面我们依次计算:
std(dim1)^2 % 得到 108.3222 std()是求标准差的函数
std(dim2)^2 % 得到 260.6222
std(dim3)^2 % 得到 94.1778
这样,我们就得到了计算协方差矩阵所需要的所有数据,调用Matlab自带的cov函数进行验证:
cov(MySample)
=
简化算法:
由于分别为m 与n 个标量元素的列向量随机变量X 与Y,二者对应的期望值分别为μ与ν,这两个变量之间的协方差定义为m×n
矩阵
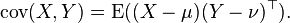
也就是说,先让样本矩阵中心化,即每一维度减去该维度的均值,使每一维度上的均值为0,然后直接用新得到的样本矩阵乘上它的转置,然后除以(N-1)即可。即为上式。N 表示的是每一维度的样本数。
例子:
X’=[1 2 3 ] %均值是2
Y’=[4 5 6] %均值是5
则会得到 x-2=[-1 0 1]’ ; y-5=[-1 0 1]’
进行转置相乘后 求均值
则得到 ((x-2)’*(y-5))/2=[1 1;1 1] 同结果是一样的
再举个例子:
a=fix(rand(10,3)*50)
a =
37 42 17
12 12 41
25 40 29
34 12 27
44 46 45
47 17 14
27 9 37
6 12 37
7 30 19
12 23 28
x=a-repmat(mean(a),10,1)%这里mean(a)得到的是列平均值,repmat(mean(a),10,1)是产生一个10行一列的矩阵。在这里的一列是指mean(a)整体
x =
11.9000 17.7000 -12.4000
-13.1000 -12.3000 11.6000
-0.1000 15.7000 -0.4000
8.9000 -12.3000 -2.4000
18.9000 21.7000 15.6000
21.9000 -7.3000 -15.4000
1.9000 -15.3000 7.6000
-19.1000 -12.3000 7.6000
-18.1000 5.7000 -10.4000
-13.1000 -1.3000 -1.4000
(x’*x)./ (size(x,1)-1) =
232.9889 70.0778 -31.9333
70.0778 200.6778 -17.2444
-31.9333 -17.2444 111.1556
 延陵明天
延陵明天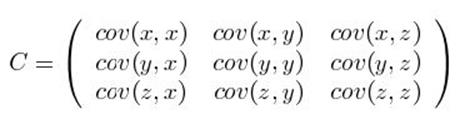




呵呵 抱歉,现在才回复。谢谢指点,我其实是新手,我稍后会验证下你的说法
不用repmat,用bsxfun函数。在矩阵较大时更节约内存~